| Les
arguments
contre l'hypothèse de la Lune |
Voici le message original
posté sur le
forum de sightings.com [9]:
"From UFO
UpDates-Toronto
Hi Bob,
I sent an e-mail request to NOAA for any other images of the full Earth
they have which also include the Moon in the same pictures.
Until then, let's do a quick mathematical check to see if the alleged
UFO Mother Ship was in fact the Moon.
The mean diameter of the Moon: 3475 km
The mean diameter of the Earth: 12,756 km
The mean distance of the Moon to the Earth: 384,500 km
The approximate distance of NOAA's GOES satellite to the Earth (since
it is in geostationary orbit): 35,786 km
The approximate distance of NOAA's GOES satellite to the Moon (since
the Moon is on the opposite side of the Earth with respect to GOES,
this will be 384,500 plus 35,786 or): 420,286 km
From trigonometry we get:
tan X(M) = 3475/420,286 = 8.268 x 10^-3 and tan X(E) = 12,756/35,786 =
3.564 x 10^-1
where X(M) is the angular size of the Moon and X(E) is the angular size
of the Earth.
From the inverse tans we get:
X(M) = 0.47 degrees and X(E) = 19.62 degrees
The ratio in sizes of the Earth to the Moon in the GEOS images should
be 19.62/0.47 = 41.7. In other words, the Earth should appear 41.7
times larger.
The diameter of the Moon (long axis) on one GEOS images I downloaded
was about 3 mm (plus or minus 0.5 mm) and the diameter of the Earth was
96 mm (plus or minus 1.0 mm). This gives ratios as large as 97/2.5 =
38.8 or as small as 95/3.5 = 27.1.
Observations:
The object in the GEOS images is smaller than what we would expect for
the Moon (assuming there is no pronounced distortions near the edges of
the GEOS images).
Nick Balaskas Physics
and Astronomy York
University "
En résumé,
d'après ses
calculs et ses données, le rapport des angles apparents de
la
Terre et de la Lune est de 41.7 et le rapport des longueurs
effectivement mesurées sur l'image de GOES du 21/11/1999
donne
au plus 38.8 et au moins 27.1 en tenant compte des marges d'erreurs sur
les mesures. Sa conclusion est que l'objet ne peut pas être
la
Lune puisque le rapport calculé (41.7) est en dehors des
limites
mesurées (inf 21.7 et sup 38.8). L'objet serait donc "trop
gros"
pour être la Lune.
Les calculs sont tout
à fait corrects
mais une des données n'est pas correcte. La distance
satellite-Lune le 21/11/99 est de 402000 km (d'après
Célestia). Cette erreur ne change pas grand chose au
résultat final.
L'erreur qui a la plus grande
influence vient
de l'oubli des rayons de la Terre et de la Lune dans l'estimation des
distances au satellite.
- Rayon de la Lune (Rl) : 1737 km
- Rayon de la Terre (Rt) : 6378 km
- Distance Satellite-Terre : 35800 + Rt = 42178 km
- Distance Satellite-Lune : 402000 + Rl = 403737 km
On calcul (en utilisant Thales) la taille qu 'aurait la
Lune(TL) si elle se trouvait à 42178 km de la Terre : TL =
(1737/403737)x42178 = 181.5 km
Le rapport R de la taille de la Lune (TL) et de celle de
la
Terre (TT) nous donne : R= TT/TL = 6378/181.5 = 35.1
On trouve alors un rapport qui se trouve tout
à fait
dans les limites de ce qui a été
mesuré sur
l'image satellite. L'hypothèse de la Lune est
toujours
valable.
| Un
problème de durée de visibilité |
Les satellites GOES prennent une
image toutes
les 30 minutes. Or, l'objet est présent sur une image mais
est
absent sur la précédente et la suivante. Cela
veut dire
qu 'il n'est"resté" que quelques dizaine de minutes. Les
tenants
de cet argument nous annoncent alors que la Lune ne se
déplaçant que d'une douzaine de degrés
par jour,
elle n'aurait pu quitter l'image aussi rapidement.
Cet argument, qui n'exprime que
la
méconnaissance des bases de la mécanique
céleste
de son auteur, ne tient pas si l'on considère les mouvements
respectifs de la Lune et du satellite.
En effet, en quelques dizaines de
minutes la
Lune n'a pas beaucoup bougée mais le satellite si. Les
satellites GOES sont géostationnaires. Cela veut dire qu 'il
tourne à la même vitesse que la Terre soit
360° en 24
h. En 30 minutes, le satellite s'est donc déplacé
de
7.5°. Ces 7.5° font que la Lune était hors
champ sur
l'image précédente et cachée
derrière la Terre sur l'image suivante. Il
est fort
dommage que les archives de la NOAA ne remontent pas jus qu'en 1999 car
il aurait été intéressant d'avoir
l'image de 15h45
car la Lune aurait dû réapparaître de
l'autre
côté de la Terre. Voici la séquence de
trois image
reconstituées :
| Le
problème de la présence de la Lune sur l'image du
canal 3 |
Pour certaines personnes, la Lune
ne peut pas
apparaître sur des photos satellites détectant la
présence de vapeur d'eau à moins qu 'il n'y ait
beaucoup
d'eau sur la Lune.
Les satellites GOES observent la
Terre dans
plusieurs longueurs d'ondes.
|
Canal
|
Gamme
spectrale
(micromètres)
|
Fonction
principale
|
|
1
|
0.55-0.75
|
Observation des nuages le
jour
|
|
2
|
3.8-4
|
Observation du brouillard
la nuit et
des feux le jour
|
|
3
|
6.5-7
|
Surveillance de la vapeur
d'eau
atmosphérique
|
|
4
|
10.2-11.2
|
Observation des nuages la
nuit
|
|
5
|
11.5-12.5
|
Observation des nuages la
nuit
|
Le canal trois est sensible
à la vapeur
d'eau et certaines personnes s'étonnaient donc de pouvoir
voir
la Lune dans un tel canal.
Ce qu 'il faut comprendre c'est
que n'importe
quel corps porté à une certaine
température
rayonne dans un grand domaine de longueur d'onde [4].Comme on le voit
sur le graphique ci-dessous, un corps porté à 400
K, 350
K ou 300 K a un maximum de rayonnement dans les longueurs d'ondes
micrométriques (donc évidemment à 6.5
micromètres !).
Le radiomètre du
satellite est sensible
au flux lumineux émis à cette longueur d'onde.
L'électronique du satellite convertit ensuite les flux
élevés en pixels sombres et les flux faibles en
pixels
clairs. On en déduit la classification suivante :
- Pixel clair <--> Température
d'émission
faible
- Pixel sombre <-->
Température
d'émission élevée
On peut alors affirmer que,
quelle que soit sa
température, la Lune va émettre dans l'infrarouge
et
produira donc un rayonnement que captera le satellite et qu 'il
convertira en niveau de gris. Il n'y a pas besoin d'eau
sur la
Lune pour qu 'elle émetteà 6.5
micromètres.
Ceci explique que la
Lune peut
être présente sur les images infrarouge.

| Le
problème de l'apparence de la Lune |
Les tenants d'un objet non
identifié
ont exprimé l'argument que la forme de l'objet permet
d'exclure
l'hypothèse de la Lune. En effet, on peut observer sur les
photos de droite et de gauche que l'objet est plutôt de forme
elliptique alors que la Lune devrait être beaucoup plus
arrondie
(simulation du centre).
|
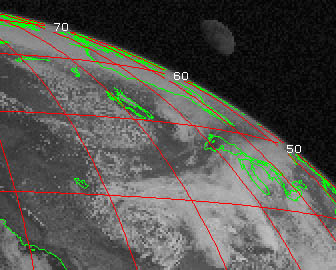
Forme de la
Lune dans le visible
sur la photo satellite
|
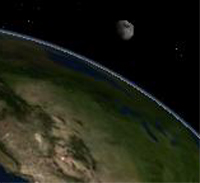
Forme de la
Lune sur une
simulation (au même instant) de Célestia.
|
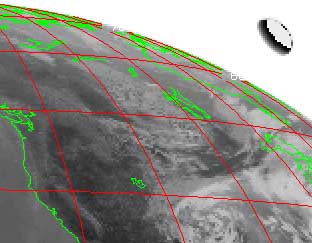
Forme de la
Lune dans
l'infrarouge sur la photo satellite
|
Dans un premier temps, la forme
elliptique a
été expliquée par le mouvement de la
Lune pendant
le temps d'exposition de la prise de vue. En effet, si la Lune se
déplace notablement pendant la prise de vue, elle va laisser
une
traînée sur l'image [10]. Cependant, en
étudiant de
plus près la manière dont les satellites
météorologiques photographient la Terre, on se
rend
compte que la raison est toute autre et que la Lune doit
nécessairement apparaître avec une
forme
elliptique sans que cela soit un phénomène de
traînée.
Jean GAY, astronome au
département
GEMINI de l'Observatoire de la Côte d'Azur nous explique le
protocole des prises de vue par les satellites
Météosat.
Les satellites sont de forme
cylindrique et
sont en rotation autour de l'axe du cylindre. A chaque rotation, ils
photographient une bande de la Terre. Pour reconstituer une image de la
Terre, il faut réassembler ces bandes.
Cependant, après
chaque rotation du
satellite sur lui même, l'axe satellite-Terre a
changé de
place si bien que toutes les bandes se trouvent
décalées
les unes par rapport aux autres. Pour reconstituer une Terre bien
ronde, il faut introduire des corrections pour compenser ce mouvement
de la Terre (figure a). Ces corrections ne sont pas valables pour la
Lune qui ne se déplace pas à la même
vitesse que la
Terre dans le champ de vision du satellite. Chacune des bandes
représentant la Lune est déplacée mais
pas de
manière adéquate pour reformer un cercle. L'image
formée est alors une ellipse (figure b). En voulant
reconstituer
la Terre, on déforme la Lune .
|

Figure a (Terre
reconstituée)
|

Figure b (Lune
déformée)
|
C'est donc le mode
de reconstitution
des images par le satellite qui donne cette forme
particulière
à la Lune.
| Le
problème de la "couleur" de la Lune en infrarouge |
Il n'y avait pas seulement la
forme de l'objet
qui posait problème, il y avait aussi sa couleur. Le
satellite
codant les zones chaudes en noir et les zones froides en blanc, la
partie éclairée de la Lune doit être
noire (~400 K)
et la partie située dans l'ombre doit être blanche
(~100
K). Cependant, lorsqu'on observe l'objet sur les photos, on remarque
que la partie éclairée est grise très
claire (donc
a priori très froide), que la zone de transition entre la
partie
éclairée et la partie sombre est
constituée d'une
ou plusieurs bandes dégradées (donc où
il y aurait
des variations très rapides de température).
L'objet n'a
donc pas l'apparence que devrait avoir la Lune.
C'est sans compter sur le
fonctionnement du
satellite. La lumière émise par la Lune et
reçue
par le capteur du satellite est un signal analogique qui est ensuite
converti en signal numérique par un convertisseur. Ces
convertiseurs ne fonctionnent que dans une certaine gamme de
températures. Si la température
dépasse la valeur
maximum, le convertisseur boucle et reprend à partir de la
température la plus basse de sa gamme. La
température
affichée est donc une température modulo un
intervalle
donné.
Si on considère un
satellite ayant une
gamme de température de 100 K à 200 K et des
températures variant de 100 K à 450 K, on aura
l'évolution suivante :
|
Température
réelle
|
Température
après
traitement dans le convertisseur
|
|
100 K
|
100 K
|
|
150 K
|
150 K
|
|
200 K
|
200 K
|
|
225 K
|
125 K
|
|
250 K
|
150 K
|
|
300 K
|
200 K
|
|
325 K
|
125 K
|
|
350 K
|
150 K
|
|
400 K
|
200 K
|
|
450 K
|
250 K
|
On va maintenant
considérer le cas de
la Lune. Le graphique ci-dessous représente les variations
de la
température lors du passage de la zone
éclairée
vers la zone sombre (trait plein), les mêmes variations de
température mais après être
passées dans le
convertisseur analogique numérique (trait en
pointillé)
et enfin le domaine de température du satellite.
On observe alors plusieurs
phénomènes :
- Sur la partie éclairée,
malgré une
température très élevée le
codage
donné par le satellite sera une couleur gris-clair.
- Lors du passage vers la zone sombre, la
température
donnée par les convertisseurs va descendre puis remonter
faisant
ainsi apparaître des bandes dégradées
du noir au
blanc.
- Dans la partie non éclairée, on
retombe dans
le domaine de température du satellite et la couleur diminue
définitivement jusqu'au blanc.
On obtient donc la succession de
couleurs
suivante :
On peut alors comparer aux
différentes
images d'ovnis et constater que l'on retrouve cette succession de
couleurs. Seul le nombre de bandes change selon le domaine de
température dans la longueur d'onde choisie.
On peut ajouter aussi que
lorsqu'il y a
plusieurs bandes, les dégradés ne sont pas
très
réguliers car la définition de l'image n'est pas
bonne
(pixélisée).
Il n'y a donc pas
besoin de faire appel
aux soucoupes volantes pour justifier ces images. La Lune suffit.
Certaines personnes ont aussi
pensé
à un canular en faisant remarquer que sur les photos, on
distingue un carré autour de l'objet comme si celui ci avait
été découpé puis
ajouté sur l'image.
Cet effet de "carré"
vient en fait de la
compression de l'image. Comme on peut le voir sur l'exemple suivant que
j'ai reconstitué, le dessin initial est net mais une fois
compressé on voit apparaître un carré
autour. Cette
compression a été réalisée
à l'aide
d'Adobe Photoshop 5.5.
|
|
|
|
|
Dessin original
|
Dessin
compressé
|
Dessin
compressé grossi
|
Cette étude nous montre que les
arguments
avancés par les "soucoupistes" sont basés, pour
la
plupart, sur des erreurs de calculs ou sur des ignorances des principes
de fonctionnement des instruments d'observation et de la
mécanique céleste.
Avant de vouloir étudier le
fonctionnement des
soucoupes volantes, de calculer leur vitesse de déplacement,
de
mesurer leur taille, de savoir si elles ont des hublots ou si elles
rejètent de la vapeur d'eau, il faudrait peut être
mieux
étudier d'un peu plus près les rouages de nos
"vulgaires"
satellites d'observations et de comprendre de quelle manière
ils
nous montrent notre planète Terre. Cela nous permettra
à
l'avenir de reconnaître, même lorsqu'elle
apparaît de
manière fugitive sur quelques clichés, son
satellite,...
LA LUNE !
Jérôme
BELLAYER
Laboratoire de Zététique
Retour
Documentation
:
Z-Files
|